Introduction

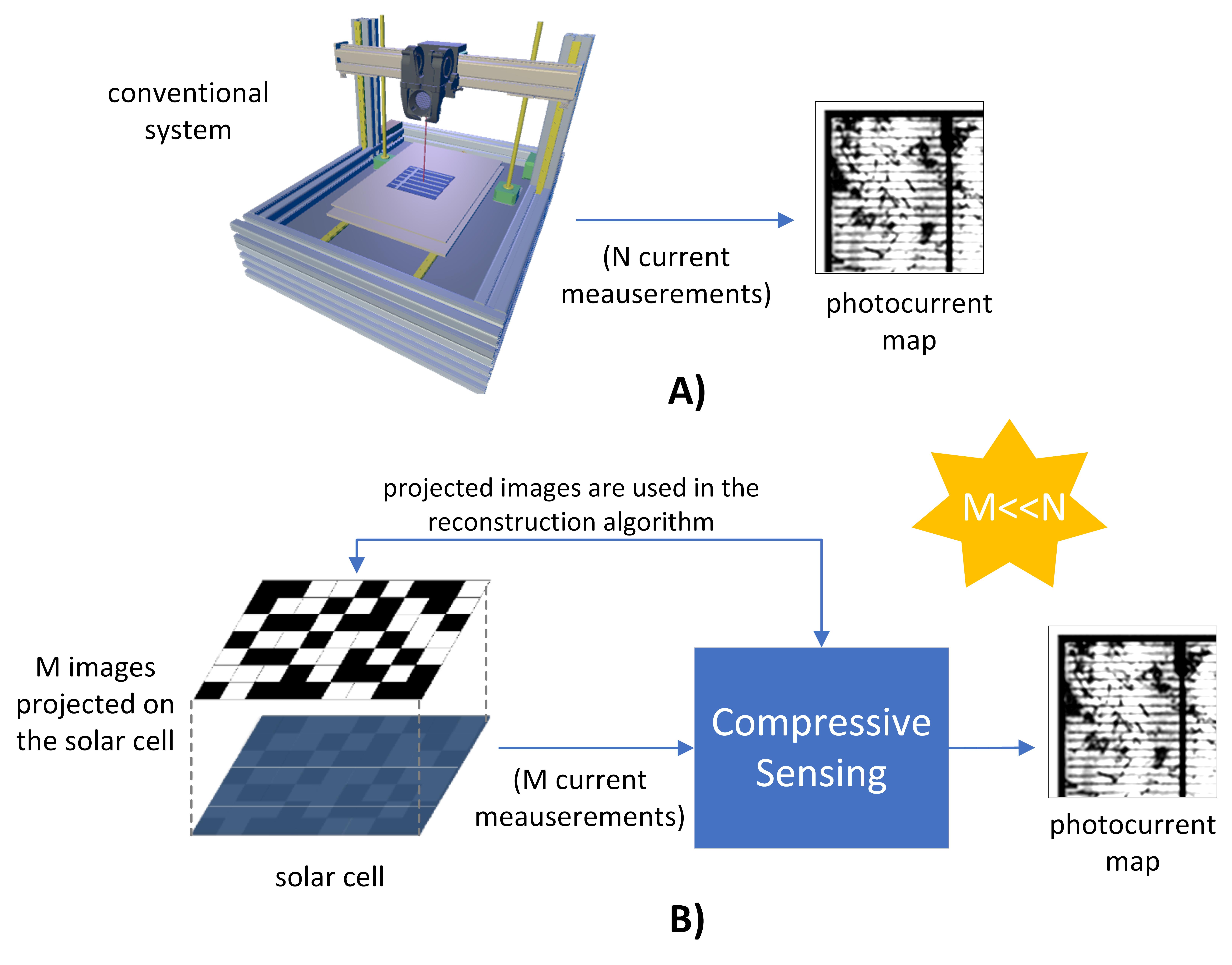
Photocurrent mapping (PM) is a non-destructive characterization method of solar cells and panels. It is used in the industry for quality control in the production of photovoltaic devices, in scientific laboratories to characterize new materials, and in photovoltaic facilities to find module failures. The PM consists of applying a laser light beam perpendicularly on a photovoltaic device, scanning the surface point by point, and measuring the induced current as a function of the position of the beam (Figure A). These systems require a high degree of mechanical stability, which leads to an increase in the characterization times when the area is large. In recent years, it has been made progress in the use of compressive sensing algorithms applied in PM tests (Figure B) in order to reduce moving parts and the measuring times. In this work we apply the compressive sensing technique to obtain a photocurrent map of Si photovoltaic devices. Results are compared with the ones obtained by the conventional technique.

In recent years, it has been made progress in the use of compressive sensing algorithms applied in PM tests in order to delimit the use of moving parts and reduce the measuring times. The objective of this project was to design and implement a compressive photocurrent mapping system for photovoltaic devices based on a projector and the use of compression sensing algorithms.

Problem formulation

The signal $x$ is called K-sparse in $\Psi$ basis if only $K$ components of the vector $s$ are non-zero and the others, i.e. $N-K$ components, are zero. If one could know in advance in which base the signal to be measured is sparse, it would be sufficient to measure the $K \ll N$ values corresponding to the coefficients of the signal in that base, i.e. it would be sufficient to make $K$ measurements. We denote $y_j$ ($j=1,\dots,M$) as each of the measurements of the signal $x$. Each measurement will be a linear combination of the values of $x$, so it can be thought of as an inner product between $x$ and a vector $\phi_j$ ($j=1,\dots,M$). Rearranging the vectors $\phi_j$ in the rows $\phi_j^T$ forms a matrix $\Phi \in \mathbb{R}^{M\mathrm{x}N}$ called measurement matrix. Substituting, we obtain: \begin{equation} y=\Phi x = \Phi\Psi s=\Theta s \end{equation} The matrix $\Theta \in \mathbb{R}^{M\mathrm{x}N}$ must satisfy two conditions: the principle of restricted isometry and the incoherence property. The direct construction of the matrix $\Phi$ such that $\Theta=\Phi\Psi $ fulfills both conditions is very difficult to achieve, however both can be achieved with high probability by means of a random $\Phi$ matrix of Bernouli type.

Once $\Phi$ has been defined and the $M$ measurements have been made, the algorithm should be able to obtain the values of the vector $s$ by solving the inverse problem $y = \Theta s$. This is an ill-conditioned problem, i.e., there are many and significantly different solutions, so the algorithm is asked to impose some constraint on $s$. Two alternatives are examined next: minimizing the $l_1$ norm and minimizing the Total Variation (TV). After the minimization process, the map corresponding to the photovoltaic device $x$ is obtained by $x = \Psi s$.

CS System

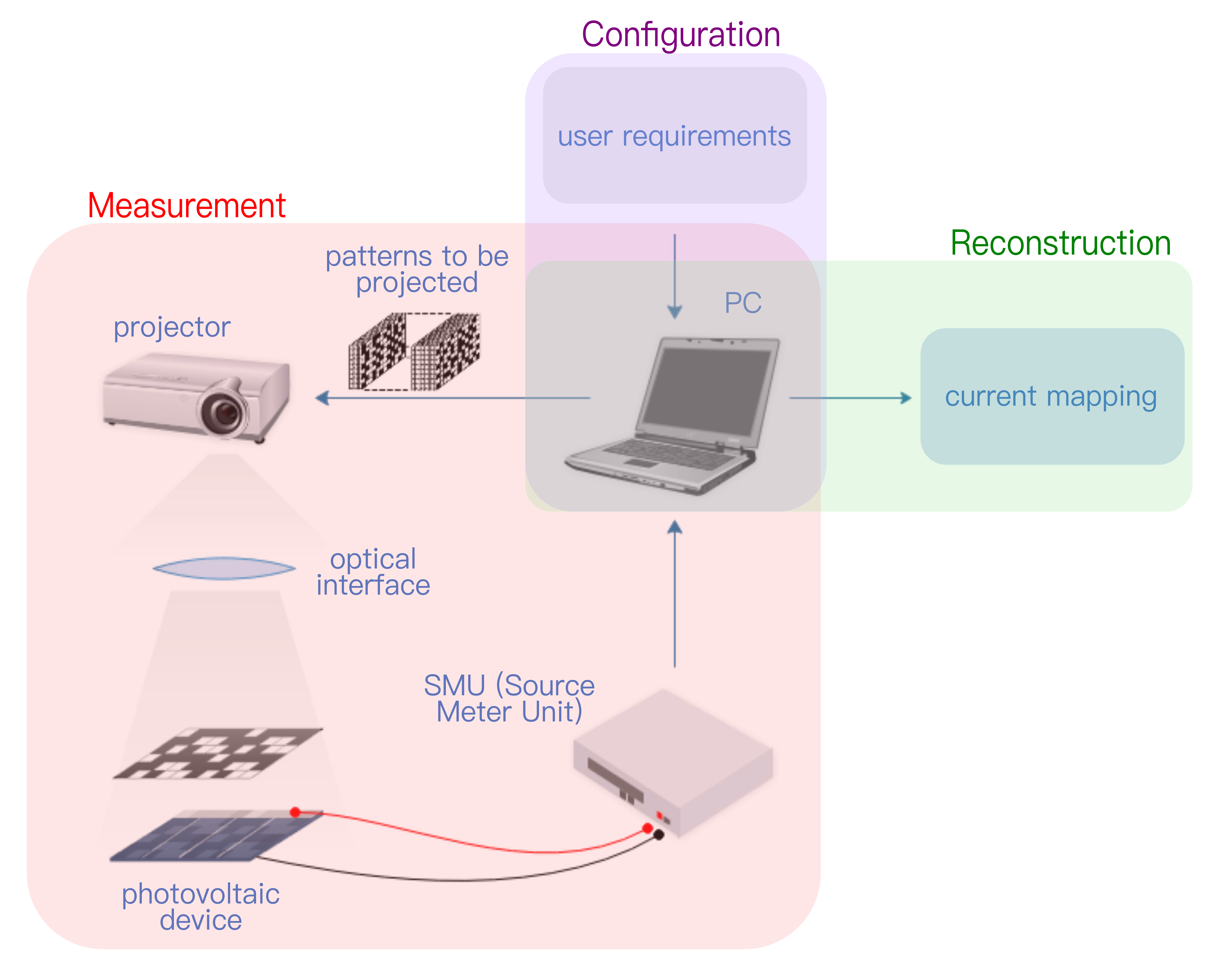
The scheme of experimental set-up is shown in the next figure, where the three stages are displayed in different colors.

The user starts a measurement using the graphical interface stored in the computer (PC). The projector is used for imaging the patterns on the cell. A lens is used to modify the size of projected patterns. Finally, the current values are obtained by a SMU (Source Meter Unit) Keithley 2400 and stored in the PC. After this process, an optimization algorithm returns the photocurrent map throw a minimization function.

a) Measurement process

The measurement process consist of obtaining $M$ measurements of a signal $x$, which in this case represents the photocurrent map of the cell. Each measurement is obtained by performing the product between the signal $x$ and a matrix $\phi_j$ ($j=1,\dots,M$). Each one of these $M$ matrices has 64 rows by 64 columns and is randomly generated with values 1 and 0. In turn, this matrix is equivalent to an image called \emph{pattern} that consists of small squares called \emph{pixels}. A black pixel corresponds to the value 0, and similarly a white pixel corresponds to 1. The randomly generated pattern is projected onto the solar cell.

Next figure shows the measurement process represented in mathematical form, in order to visualize the relationship between the measurement process and the mathematical problem to be solved. In this figure the process is carried out as an example taking $M=4$ measurements by means of four 3x3 patterns. In the following section the results are shown in real samples using 64x64 patterns.

The purple square represents the actual PM of cell $x$ which is rearranged as a column vector. The projected patterns, or equivalently the $\phi_j$ matrices, are rearranged as rows to form the measurement matrix $\Phi$. By projecting the $M$ patterns onto the cell and acquiring the $M$ photocurrent values, what is being done mathematically is a multiplication between the measurement matrix $\Phi$ and the actual PM of the cell $x$, to obtain the measurement vector $y$. Therefore, the aforementioned inverse problem $\Phi x=y$ is expressed. The latter is solved in the reconstruction process, to find the photocurrent map of the cell.

b) Reconstruction process

The mathematics involved in compressive sensing ensures that a good representation of the photocurrent map $x$ is achieved, without knowing in advance the basis on which this representation is sparse. As we saw, the inverse problem $\Phi x = y$ is reformulated as $\Phi x= \Phi \Psi s = \Theta s = y $. This new matrix $\Theta$ results from the multiplication between $\Phi$ and $\Psi$, therefore it still fulfills the necessary conditions for the compressive sensing process. Now, it remains to know which is the proper basis $\Psi$ where the PM representation is sparse.

In solar cells, the conventional shape and geometry of the contact grid is similar to horizontally and vertically distributed stripes. If there is any $\Psi$ basis whose elements are images with this kind of shapes, that would be a suitable basis, since the cell geometry could be represented with few elements. A prori it is not known in which basis the PM representation is sparse, however both the DCT (Discrete Cosine Transform) basis and the Walsh-Hadamard basis are presented as possible options, since both have the elementary shapes mentioned. Whatever the basis on which the PM is reconstructed, the measurement process is performed with the randomly generated $\Phi$ matrix. Then, depending on the basis selected by the user (DCT or Hadamard), the resulting $\theta$ matrix is generated. Therefore, it is important to note that in this CS technique, the measurement is the same regardless of the basis that is then chosen to try to reconstruct the photocurrent map. After making the $M$ measurements to form the vector $y$ and determining the basis on which it is reconstructed, it is possible to reconstruct the photocurrent map $s$ (expressed in a basis $\Psi$) by solving the problem $y = \Theta s$. Since this is an ill-conditioned inverse problem, there exist many $s$ that satisfy it, so some additional condition is imposed on $s$. For this CS system, two conditions were tested: minimize the $l_1$ norm or minimize the Total Variation (TV). The vector $s$ obtained by the algorithm is the representation of the PM of the cell in the $\Psi$ basis. What remains is to obtain the representation of the PM in the canonical basis ($x = \Psi s$).

Experimental results

Si-solar cell 1

• $M$ is the number of patterns projected during the measurement process.
• $N$ is the number of pixels each pattern has. For example, a 64x64 pattern has $N$ = 64*64 = 4096 pixels.

Si-solar cell 2

The next sample to be measured is a concentrator Si cell with 3 $ mm$ in diameter. Nex figure A shows a real photo of the sample. The conventional PM (LBIC) is shown in B whereas CS result is in C. Both results have the same resolution, in order to be able to compare the results. In the CS result, the boundary between silicon and metal can be clearly seen. As in the last case, it is possible to distinguish a contact grid.

Conclusion

In this work, a system for the characterization of photovoltaic devices without moving parts using compressive sensing techniques was designed and implemented. A graphical interface was programmed, so that it is easy for the user to perform the measurement process and obtain the PM of solar cells. Through it, it is possible to configure different measurement parameters, including the size and color of the patterns to be projected, the number of patterns for the measurement and parameters related to the communication between the PC and the SMU. To reconstruct the PM from the measurement, the SC system offers the possibility to use the TV or $l_1$ minimization algorithm and to do it in the DCT basis or in the Hadamard basis.

Acknowledgment

This work was supported by a grant from Universidad Nacional del Comahue (UNCo): PIN 2018 04/I24.

Access to paper

This work was presented at The Argentine Conference on Electronics CAE UTN-FRC Córdoba, Argentina - March 9th-10th, 2023. Also, the article is available on the IEEE Website (link below).

See the paper